Unraveling The Power Of UMAP: A Comprehensive Guide To Dimensionality Reduction

Unraveling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction

Related Articles: Unraveling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction

Introduction

With great pleasure, we will explore the intriguing topic related to Unraveling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction. Let’s weave interesting information and offer fresh perspectives to the readers.

Unraveling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction

In the realm of data analysis, navigating high-dimensional datasets poses a significant challenge. The sheer volume and complexity of features often hinder our ability to extract meaningful insights and visualize relationships. This is where dimensionality reduction techniques come into play, and among them, Uniform Manifold Approximation and Projection (UMAP) stands out as a powerful and versatile tool.

Understanding the Essence of UMAP

UMAP is a non-linear dimensionality reduction algorithm designed to preserve the global structure of data while providing a lower-dimensional representation. It excels at capturing complex relationships within high-dimensional datasets, enabling visualization and analysis that would otherwise be intractable.

The Mechanics Behind UMAP

At its core, UMAP operates on the principle of manifold learning. It assumes that high-dimensional data points lie on a lower-dimensional manifold, a continuous surface embedded in the higher-dimensional space. UMAP seeks to uncover this underlying manifold and project the data points onto it, effectively reducing the dimensionality without sacrificing crucial information.

Key Features of UMAP

1. Preservation of Global Structure: UMAP prioritizes maintaining the global structure of the data, ensuring that points that are close in the original high-dimensional space remain close in the reduced representation. This is achieved through the use of a fuzzy topological structure, allowing for a more nuanced understanding of neighborhood relationships.

2. Adaptive Neighborhood Selection: Unlike other dimensionality reduction techniques, UMAP adapts the size and shape of neighborhoods based on the local density of data points. This allows for a more accurate representation of the data, particularly in regions with varying densities.

3. Scalability and Efficiency: UMAP is designed to handle large datasets efficiently, making it suitable for real-world applications. Its computational complexity is lower compared to other techniques, allowing for faster processing and analysis.

4. Interpretability: UMAP provides a visually appealing and interpretable representation of the data. The reduced dimensions often correspond to meaningful features or relationships, aiding in understanding the underlying structure of the dataset.

UMAP in Action: Real-World Applications

UMAP’s versatility makes it applicable across various fields, including:

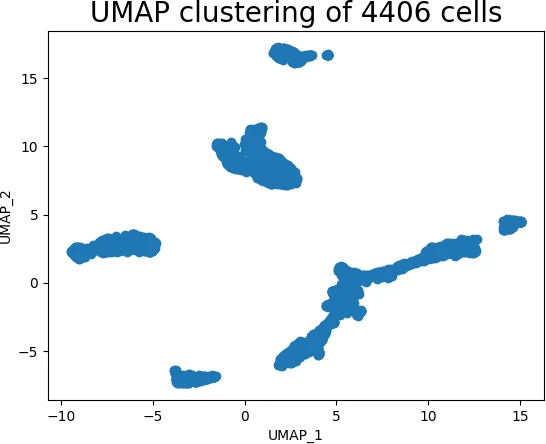
• Data Visualization: UMAP enables the visualization of high-dimensional datasets, facilitating the identification of clusters, outliers, and patterns that might be obscured in the original space.

• Machine Learning: UMAP can be used as a preprocessing step for machine learning models, reducing the dimensionality of the data and improving the performance of subsequent algorithms.

• Bioinformatics: UMAP is employed to analyze gene expression data, identifying distinct cell types and understanding cellular processes.

• Image Processing: UMAP helps in analyzing and visualizing image data, extracting features and identifying patterns that might be missed by traditional methods.

• Text Analysis: UMAP can be used to analyze text data, identifying topics, clusters of documents, and relationships between words.

Beyond the Basics: Advanced UMAP Concepts

• Metric Selection: UMAP allows for the selection of different metrics to measure distances between data points. The choice of metric can significantly impact the results, and careful consideration should be given to the nature of the data and the desired outcome.

• Parameter Tuning: UMAP offers various parameters that can be adjusted to fine-tune the dimensionality reduction process. These parameters include the number of neighbors, the minimum distance, and the target dimensionality.

• Integration with Other Techniques: UMAP can be combined with other dimensionality reduction techniques, such as Principal Component Analysis (PCA), to achieve a more comprehensive analysis.

Frequently Asked Questions about UMAP

Q: What are the limitations of UMAP?

A: While UMAP is a powerful tool, it is important to acknowledge its limitations. UMAP is not always able to perfectly preserve the original structure of the data, especially in cases of highly complex or noisy datasets. Additionally, the choice of parameters can significantly influence the results, requiring careful consideration and experimentation.

Q: How does UMAP compare to other dimensionality reduction techniques?

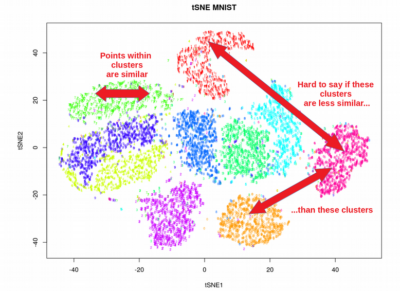
A: UMAP offers several advantages over traditional techniques like PCA and t-SNE. Compared to PCA, UMAP is more robust to non-linear relationships and can handle complex datasets. Compared to t-SNE, UMAP is more scalable and offers a more global perspective of the data, while t-SNE focuses on local relationships.

Q: Can UMAP be used for both supervised and unsupervised learning?

A: UMAP is primarily used for unsupervised learning, as it does not require labeled data. However, it can also be used in supervised learning settings, where it can be applied to the input features of a model, potentially improving its performance.

Tips for Effective UMAP Application

• Data Preprocessing: Ensure the data is properly preprocessed before applying UMAP. This includes handling missing values, scaling features, and removing irrelevant variables.

• Parameter Tuning: Experiment with different parameters to find the optimal settings for your specific dataset. Consider using cross-validation techniques to assess the performance of different parameter choices.

• Visualization: Utilize visualization tools to interpret the results of UMAP. Create scatter plots, heatmaps, or other graphical representations to gain insights into the reduced representation of the data.

• Domain Expertise: Incorporate domain expertise into the analysis to interpret the results in the context of the problem at hand.

Conclusion: Embracing the Power of UMAP

UMAP stands as a powerful tool for dimensionality reduction, offering a unique blend of scalability, interpretability, and preservation of global structure. Its ability to uncover hidden patterns and relationships within complex datasets makes it invaluable for data visualization, machine learning, and various other fields. By embracing UMAP, researchers and analysts can unlock new insights and gain a deeper understanding of the data they work with, ultimately driving innovation and progress.

Closure

Thus, we hope this article has provided valuable insights into Unraveling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction. We hope you find this article informative and beneficial. See you in our next article!